| Summary | |
|---|---|
| MENU |
An instance of ADT Dictionary stores entries each of which is
a pair (k,e) of a key k and an item e.
Let Key and Item denote ADTs for keys and items, respectively,
which could be anything depending on applications.
Note that the ADT Key must have at least a method for equality
testing.
There are two kinds of dictionaries.
o unordered dictionary
o ordered dictionary
The ordered dictionary is regarded as a specialization of
the unordered dictionary, where additional methods are provided
in order to refer to the ordering of entries.
Note that the ADT Key used in the ordered dictionary must have
appropriate comparison methods besides the equality testing.
public class Dictionary
{ /* This is ADT whose instances are unordered dictionaries.
Assume that there may be multiple entries with the same key,
although there is a unique entry of the same pair (k,e).
NO_SUCH_KEY is a special instance (so-called a sentinel)
of ADT Item which denotes that the search was unsuccessful.
SequenceItems is ADT whose instances are sequences of items.
*/
public Dictionary( )
{Create an instance of ADT Dictionary and initialize it
to be empty.}
public int size( )
{Return the number of entries in this instance.}
public Item getItem(Key k)
{If there is at least one entry with a given key k
in this instance, return an item of such an entry
(an arbitrary entry with the key k if there are
multiple entries with k).
If there is no entry with the key k in this instance,
return a sentinel NO_SUCH_KEY.
public SequenceItems getAllItem(Key k)
{Return a sequence of items which is an enumeration of
all items with a given key k in this instance.
Note that it returns a null sequence in case of
unsuccessful search.}
public void insertItem(Key k, Item e)
{Insert a new entry which is a pair of key k and item e
into this instance.}
public void deleteItem(Key k, Item e)
{If there is an entry (k,e) in this instance,
delete the entry from this instance.
Otherwise, do nothing.}
public void deleteAllItem(Key k)
{Delete all items with a given key from this instance, if any.}
}
An ADT for ordered dictionaries can be defined as a subclass of
the above ADT Dictionary by giving the following additional methods,
where Entry is ADT whose instances are pairs of keys and items.
public Entry getNext(Key k, Item e)
{Assume that a given entry (k,e) is in this instance.
If (k,e) is not the last entry in the ordering of this instance,
return the next entry of (k,e) in this dictionary.
Otherwise, return a sentinel NO_SUCH_ENTRY.}
public Entry getPrevious(Key k, Item e)
{Assume that a given entry (k,e) is in this instance.
If (k,e) is not the first entry in the ordering of this instance,
return the previous entry of (k,e) in this dictionary.
Otherwise, return a sentinel NO_SUCH_ENTRY.}
public Key getClosestNextKey(Key k)
{If k is not largest in this instance, return the key
which is smallest among those keys larger than k
in this instance.
Otherwise, return a sentinel NO_SUCH_KEY.}
public Key getClosestPreviousKey(Key k)
{If k is not smallest in this instance, return the key
which is largest among those keys smaller than k
in this instance.
Otherwise, return a sentinel NO_SUCH_KEY.}
There are at least two major implementations of ADT Sequence.
Namely, array implementation and linked list implementation.
Depending on which search algorithm on ADT Sequence
is used for ADT Dictionary,
different implementations of ADT Dictionary are analyzed as follows.
2.1 Sequential Search
Complexity Measure = No. comparisons between the search object z
^^^^^^^^^^^
(called probes)
and some entry in a dictionary being searched
pi = probability that z = xi
where xi is the i-th entry in the dictionary
-----------------------------------------------------------------------
Worst Best Average
-----------------------------------------------------------------------
successful search n 1 ∑ni=1 (i pi)
depending on the order of entries
-----------------------------------------------------------------------
unsuccessful search n n n
-----------------------------------------------------------------------
Fact ∑ni=1 (i pi) is minimized when p1 ≥ p2 ≥ ... ≥ pn.
pi is usually unknown.
--> Changing dynamically the order of entries so that
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
(self-organizing)
entries frequently accessed move toward the front of the dictionary
while those infrequently accessed move toward the rear
o Move-ahead-one strategy
o Interchange-to-the-front strategy
o Move-to-front strategy
The time complexity for unsuccessful search can be reduced by
maintaining the dictionary in some natural order.
---> Exploit the fact that z>xi implies
z>xj for all 1≤j≤i.
---> Binary Search
-------------------------------------------------------------------------
Worst Best Average
-------------------------------------------------------------------------
successful ceiling(lg(n+1)) 1 (1+1/n)lg(n+1)+o(1)
-------------------------------------------------------------------------
unsuccessful ceiling(lg(n+1)) floor(lg(n+1)) lg(n+1)+o(1)
-------------------------------------------------------------------------
Binary search requires the direct access to all parts of the ordered
dictionary.
---> Linked list representation cannot be used.
---> Modification of the ordered dictionary is not easy.
Average-Case Analysis of Binary Search
--------------------------------------
Extended Binary Trees
- A left or right child called an external vertex is added to
a vertex in the decision tree of binary search if the vertex
does not have the left or right child, respectively.
Example
-------
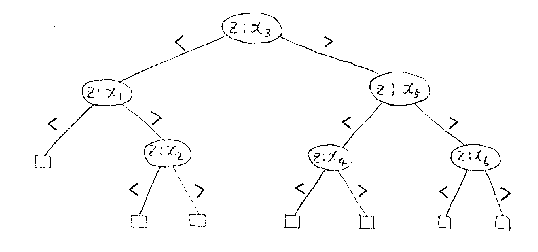
An external vertex represents that a search is unsuccessful.
An internal vertex represents that a search is successful if
the search stops at that vertex.
Definitions
-----------
T: Extended binary tree with n internal vertices
(and hence n+1 external vertices)
External Path Length E(T) = the sum of levels of all the
external vertices
Internal Path Length I(T) = the sum of levels of all the
internal vertices
Average Number of Comparisons in Unsuccessful Search
Un = E(T)/(n+1) assuming uniform probability
Average Number of Comparisons in Successful Search
Sn = I(T)/n assuming uniform probability
Relationship between E(T) and I(T)
----------------------------------
D(T)=E(T)-I(T)=2n
---> I(T)=E(T)-2n
---> It is sufficient to find E(T).
Range of a Value of E(T)
------------------------
Maximum Value of E(T) = n(n+3)/2
-------------
(Proof) Show that the tree shown below has the maximum E(T)
among all extended trees with n internal vertices.
o
/ \
/ \
o _
/ \ |_|
/ \
o _
/ \ |_|
. \
. _
. |_|
/
o .
/ \ .
/ \ .
o _
/ \ |_|
/ \
_ _
|_| |_|
Without loss of generality, we can assume that if an internal
vertex has only one internal vertex as its child, then the
child is the left child. (why?)
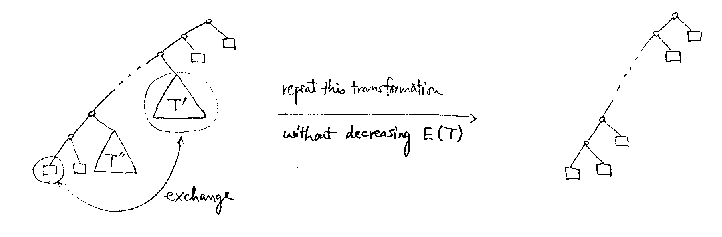
Minimum Value of E(T)
-------------
Observation 1: If T has the minimum value of E(T) among
extended binary trees with n internal vertices,
every external vertex in T is of level either
j or j+1 for some j.
(Note that j+1 must be the height h of the tree.)
Such a tree is called a completely balanced
binary tree.
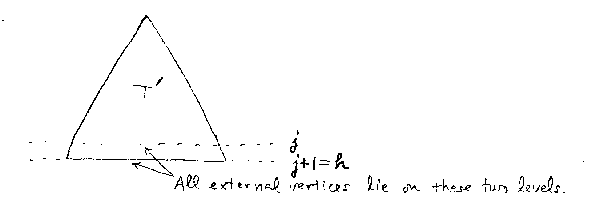
Observation 2: If j1 , j2 , ... , jn+1 are
the levels of n+1 external vertices, then
∑i=1n+1 2-ji =1.
By Observation 1, suppose that there are k external vertices
on level j and (n+1-k) on level j+1 (1 ≤ k ≤ n+1).
By Observation 2,
∑ki=1 2-j + ∑i=k+1n+1 2-j-1
= k 2-j + (n+1-k) 2-j-1 = 1.
---> k(2-j - 2-j-1) = 1 - (n+1) 2-j-1
k(21 - 20) = 2j+1 - (n+1)
k= 2j+1 -n-1
Since k ≥ 1, 2j+1 -n-1 ≥ 1.
---> 2j+1 > n+1
Since k ≤ n+1, 2j+1 -n-1 ≤ n+1.
---> 2j+1 ≤ 2(n+1)
---> 2j ≤ n+1
Thus 2j ≤ n+1<2j+1.
---> j = floor( lg(n+1) )
---> k = 2floor(lg(n+1))+1 -n-1
Minimum E(T)=jk+(j+1)(n+1-k)
=(n+1)j+(n+1)-k
=(n+1) floor(lg(n+1)) + (n+1)
- (2floor(lg(n+1))+1 -n-1)
=(n+1) floor(lg(n+1)) + 2(n+1)
- 2floor(lg(n+1))+1
Let θ = lg(n+1) - floor( lg(n+1) ),
where 0 ≤ θ < 1.
Minimum E(T)=(n+1) lg(n+1) + (n+1)(2 - θ - 21-θ)
^^^^^^^^^^^^
small if 0 ≤ θ < 1
Observation 3: An extended tree for binary search is
completely balanced.
---> E(T) = Θ(n log n)
---> Un = E(T)/(n+1) = Θ(log n)
Sn = I(T)/n = Θ(log n)
Average Time Complexity of Binary Search = Θ(log n)
for uniform probability
---> Conflict between fast search and easy modification
So far we have considered only access probabilities as information
available for analysis of search algorithms.
There are other useful statistical properties of entries.
E.g., distribution of entries in a dictionary.
Example The name "Smith" in a phone directory would be found
------- near at the third-quarters point if it is in the directory.
^^^^^^^^^^^^^^^^^^^^
Expected location implied by distribution
To begin a search nearer to the expected location of
the searched object
---> Interpolation Search
--------------------------------------
Worst Best Average
--------------------------------------
successful n 1 lg(lg n)
--------------------------------------
unsuccessful n 2 lg(lg n)
--------------------------------------
Remark
------
The average case analysis for interpolation search is different
from that considered for either sequential or binary search.
The average is taken over search objects and dictionaries
^^^^^^^^^^^^
whose entries follow a certain distribution.
Binary Search vs Interpolation Search
-------------------------------------
Experiments suggest that interpolation search is inferior to
binary search unless a dictionary is very large.
Cost per probe in interpolation search is much larger than
that in binary search.
For a large dictionary, use a hybrid method of interpolation search
and binary search.
Interpolation search at least for the first few probes will pay off.